|
FFT可以將一個信號變換到頻域���。有些信號在時域上是很難看出什么特征的,但是如果變換到頻域之后��,就很容易看出特征了��。這就是很多信號分析采用FFT變換的原因�����。另外����,F(xiàn)FT可以將一個信號的頻譜提取出來����,這在頻譜分析方面也是經(jīng)常用的����。
知識點
1、FFT——離散傅里葉變換(DFT)的快速算法���。它是根據(jù)離散傅氏變換的奇����、偶�、虛��、實等特性���,對離散傅立葉變換的算法進(jìn)行改進(jìn)獲得的�。
2���、假設(shè)采樣頻率為Fs���,信號頻率F,采樣點數(shù)為N�。那么FFT之后結(jié)果就是一個為N點的復(fù)數(shù)。每一個點就對應(yīng)著一個頻率點。這個點的模值��,就是該頻率值下的幅度特性�����。
3����、假設(shè)采樣頻率為Fs,采樣點數(shù)為N�,做FFT之后,某一點n(n從1開始)表示的頻率為:Fn=(n-1)*Fs/N�;該點的模值除以N/2就是對應(yīng)該頻率下的信號的幅度(對于直流信號是除以N);該點的相位即是對應(yīng)該頻率下的信號的相位�����。相位的計算可用函數(shù)atan2(b,a)計算�����。atan2(b,a)是求坐標(biāo)為(a,b)點的角度值��,范圍從-pi到pi�����。要精確到xHz,則需要采樣長度為1/x秒的信號����,并做FFT。要提高頻率分辨率�,就需要增加采樣點數(shù),這在一些實際的應(yīng)用中是不現(xiàn)實的��,需要在較短的時間內(nèi)完成分析�����。解決這個問題的方法有頻率細(xì)分法��,比較簡單的方法是采樣比較短時間的信號���,然后在后面補(bǔ)充一定數(shù)量的0,使其長度達(dá)到需要的點數(shù)�����,再做FFT����,這在一定程度上能夠提高頻率分辨力���。
4、由于FFT結(jié)果的對稱性��,通常我們只使用前半部分的結(jié)果�,即小于采樣頻率一半的結(jié)果。
代碼實現(xiàn)
準(zhǔn)備工作:安裝matplotlib包����,打開命令窗口,進(jìn)入安裝python下的scripts路徑����,輸入pip install matplotlib。安裝成功后會顯示如下圖:

其他包的安裝步驟類似����。
import numpy as np
from scipy.fftpack import fft,ifft
import matplotlib.pyplot as plt
import seaborn
#采樣點選擇1400個,因為設(shè)置的信號頻率分量最高為600Hz����,根據(jù)采樣定理知采樣頻率要大于信號頻率2倍,所以這里設(shè)置采樣頻率為1400Hz(即一秒內(nèi)有1400個采樣點)
x=np.linspace(0,1,1400)
#設(shè)置需要采樣的信號����,頻率分量有180����,390和600
y=7*np.sin(2*np.pi*180*x) + 1.5*np.sin(2*np.pi*390*x)+5.1*np.sin(2*np.pi*600*x)
yy=fft(y) #快速傅里葉變換
yreal = yy.real # 獲取實數(shù)部分
yimag = yy.imag # 獲取虛數(shù)部分
yf=abs(fft(y)) # 取模
yf1=abs(fft(y))/((len(x)/2)) #歸一化處理
yf2 = yf1[range(int(len(x)/2))] #由于對稱性�����,只取一半?yún)^(qū)間
xf = np.arange(len(y)) # 頻率
xf1 = xf
xf2 = xf[range(int(len(x)/2))] #取一半?yún)^(qū)間
#原始波形
plt.subplot(221)
plt.plot(x[0:50],y[0:50])
plt.title('Original wave')
#混合波的FFT(雙邊頻率范圍)
plt.subplot(222)
plt.plot(xf,yf,'r') #顯示原始信號的FFT模值
plt.title('FFT of Mixed wave(two sides frequency range)',fontsize=7,color='#7A378B') #注意這里的顏色可以查詢顏色代碼表
#混合波的FFT(歸一化)
plt.subplot(223)
plt.plot(xf1,yf1,'g')
plt.title('FFT of Mixed wave(normalization)',fontsize=9,color='r')
plt.subplot(224)
plt.plot(xf2,yf2,'b')
plt.title('FFT of Mixed wave)',fontsize=10,color='#F08080')
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
實現(xiàn)結(jié)果
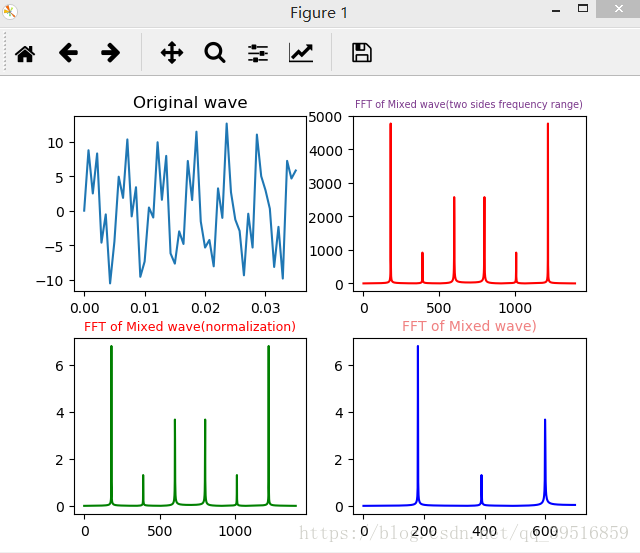
結(jié)果驗證
假設(shè)我們有一個信號�����,它含有一個頻率為180Hz�����,幅度為7V的交流信號�;一個頻率為390Hz���,幅度為1.5V的交流信號��;一個頻率為600Hz���,幅度為5.1V的交流信號��。用數(shù)學(xué)表達(dá)式就是如下:
y=7*np.sin(2*np.pi*180*x) + 1.5*np.sin(2*np.pi*390*x)+5.1*np.sin(2*np.pi*600*x)
從圖中我們可以看到�,在第181點�、第391點、和第601點附近有比較大的值���。分別計算這三個點的模值���,結(jié)果如下:
181點: 4900
391點:1030
601點:2600
按照公式,可以計算出180Hz信號的幅度為:4900/(N/2)=384/(1400/2)=7��;390Hz信號的幅度為:1030/(N/2)=1030/(1400/2)=1.5��?����?梢?�,從頻譜分析出來的幅度是正確的�����。
注:600Hz信號的幅度異常�����,具體原因為檢查出來,后期更新���。
|